Relasi Ekuivalen
Posted in himpunan ¶ Tagged ekuvalen, himpunan, matematika, Math, partisi, relasi ¶ 10 Comments
Konsep relasi pada Matematika serupa dengan pengertian relasi pada sehari-hari. AKan saya mulai dengan definisi formal relasi
Definisi 1: Suatu relasi (biner) pada himpunan  adalah himpunan bagian
adalah himpunan bagian  dari produk cartesian
dari produk cartesian 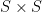 . Jika
. Jika  adalah suatu relasi dan
adalah suatu relasi dan 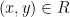 maka dikatakan
maka dikatakan  berelasi ke
berelasi ke 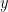 pada
pada  atau singkatnya
atau singkatnya 
Contoh 2: boleh dibilang relasi yang paling dikenal adalah relasi “=” (Sama dengan) yang memut semua elemen 
Contoh 3: Diberikan  dan
dan 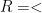 (kurang dari). Tuliskan semua elemen
(kurang dari). Tuliskan semua elemen  .
.
Diperoleh
Karena memuat semua elemen 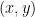 dengan
dengan 
Nah..selanjutnya kita bahas relasi ekuivalen
Definisi 4: Suatu relasi  pada himpunan
pada himpunan  dikatakan relasi ekuivalen jika memenuhi ketiga hal berikut
dikatakan relasi ekuivalen jika memenuhi ketiga hal berikut
untuk semua 
1. Reflexive 
2. Symmetry jika  maka
maka 
3. Transitive Jika  dan
dan 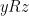 maka
maka 
Contoh 5: Diberikan himpunan  dan relasi
dan relasi  pada
pada  didefinisikan
didefinisikan  . Akan ditunjukan
. Akan ditunjukan  merupakan relasi ekuivalensi
merupakan relasi ekuivalensi
(note: 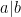 artinya
artinya  membagi
membagi 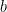 )
)
1. Reflexive. Untuk sebarang 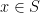 diperoleh
diperoleh 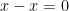 , Jelas
, Jelas  , terbukti
, terbukti  bersifat Reflexive
bersifat Reflexive
2. Symmetry. Diketahui  maka
maka  , yang artinya
, yang artinya 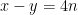 . Diperoleh
. Diperoleh 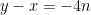 maka
maka 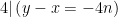 . Dapat disimpulkan
. Dapat disimpulkan 
3. Transitive. Diketaui  dan
dan 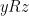 yang artinya
yang artinya
Diperoleh
Itu artinya  . Terbukti
. Terbukti  Transitive.
Transitive.
Terbukti  merupakan relasi ekuivale
merupakan relasi ekuivale
Nah yang namanya relasi ekuivalen pastilah terdapat kelas ekuivalensi, ibarat 2 sisi mata uang yang tak terpisahkan. Apa itu kelas ekuivalensi?
Definisi: Diberikan  relasi ekuivalen pada
relasi ekuivalen pada  maka untuk semua
maka untuk semua  dterdapat suatu himpunan yang berisikan semua anngota
dterdapat suatu himpunan yang berisikan semua anngota  yang berelasi ke
yang berelasi ke  , dinotasikan:
, dinotasikan:
Nah..himpunan inilah yang disebut kelas ekuivalensi
Contoh 6: Sekarang kita akan mencari kelas ekuivalensi dari contoh 5, kita akan memulai dari 1dan maju kedepan
Perhatikan bahwa kelas ekuivalensi lainnya akan sama dengan salah-satu kelas ekuivalensi diatas contohnya ![\left[1\right]=\left[5\right] \left[1\right]=\left[5\right]](http://s0.wp.com/latex.php?latex=%5Cleft%5B1%5Cright%5D%3D%5Cleft%5B5%5Cright%5D&bg=ffffff&fg=000&s=0) . Itu artinya kita telah menemukan kelas-kelas ekuivalensi yang berbeda dari contoh 5.
. Itu artinya kita telah menemukan kelas-kelas ekuivalensi yang berbeda dari contoh 5.
Perhatikan juga bahwa himpunan  terpecah menjadi 4 himpunan yang saling asing. Dengan kata lain kelas-kelas ekuivalensi membentuk partisi pada
terpecah menjadi 4 himpunan yang saling asing. Dengan kata lain kelas-kelas ekuivalensi membentuk partisi pada 
Teorema 7: Diberikan  relasi ekuivalen pada himpunan tak-kosong
relasi ekuivalen pada himpunan tak-kosong  maka kelas-kelas dari
maka kelas-kelas dari  akan mempartisi
akan mempartisi 
Nah..yang saya maksud dengan partisi adalah memecah/ membagi suatu himpunan  menjadi beberapa himpunan bagian tak-kosong yang mana setiap elemen
menjadi beberapa himpunan bagian tak-kosong yang mana setiap elemen  tepat termuat di satu himpunan bagian. Himpunan bagian ini disibut sel dari partisi. Serupa dengan partisi hardisk, tentunya mustahil suatu file termuat di dua partisi hardisk yang berbeda.
tepat termuat di satu himpunan bagian. Himpunan bagian ini disibut sel dari partisi. Serupa dengan partisi hardisk, tentunya mustahil suatu file termuat di dua partisi hardisk yang berbeda.
Jadi relasi ekuivalen adalah cara kita mempartisi suatu Himpunan. Menjadi “ekuivalen” itu berarti menjadi sama, serupa berdasarkan kriteria tertentu.
Label: Matematika

0 Komentar:
Posting Komentar
Berlangganan Posting Komentar [Atom]
<< Beranda